LeetCode-Josephu问题

题目要求

0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

输入: n = 5, m = 3
输出: 3

原题链接：剑指 Offer 62. 圆圈中最后剩下的数字

解题思路

经典的约瑟夫问题：N个人编号为1，2，……，N，依次报数，每报到M时，杀掉那个人，求最后胜利者的编号。

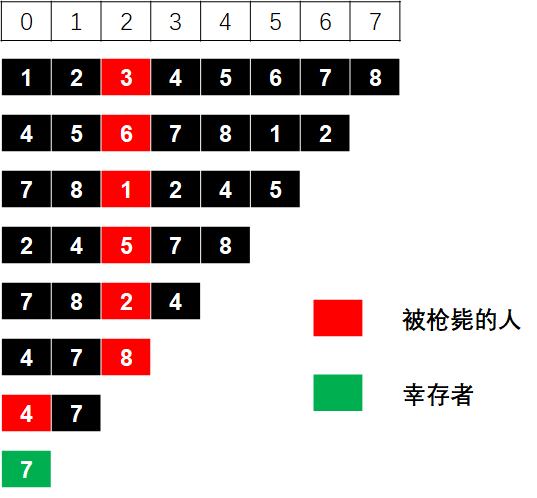
首先，这是一个典型的约瑟夫问题。本题解释以8个人，每次报3下举例。8个人编号依次为1，2，3，4，5，6，7，8.

第一次：3挂了，从编号4开始报数，可以理解为4、5、6……往左平移三个单位

第二次：6挂了，从编号7开始报数，7、8、1、2……往左平移三个单位

第三次：1挂了，从编号2开始报数，2、4、5……往左平移三个单位

第四次：5挂了，从编号7开始报数，7、8……往左平移三个单位

…….

最后剩下幸存者7。从枪毙顺序来看，每次枪毙完，后一个人开始报数，作为队列的开始进行循环。（人员左移）

现在可以逆向思维一下，通过最后一个幸存者7（幸存者一定是编号为0的），来反推这个幸存者在队列中的索引。

这可以看成一个数学表达式$f(N,M)$，其中N为队列的人数，M为报数。

则开始从幸存者开始逆推：

$f(1,3)=0$;

$f(2,3)=1$，此时队列有两个人，幸存者7整体向右位移3个单位： 1—> 0 —>1

$f(3,3)=1$，此时队列有三个人，幸存者7整体向右位移3个单位：2 —> 0 —>1

$f(4,3)=0$，此时队列有四个人，幸存者7整体向右位移3个单位：2 —> 3 —> 0

$f(5,3)=3$，此时队列有五个人，幸存者7整体向右位移3个单位：1 —> 2 —> 3

……

从上面的逆推过程就可以看出，这次的索引位置为上一次的索引位置+3再取模！

换成数学表达式就是$f(N,M)=(f(N-1),M)%N$，最后直接顺藤摸瓜，从最后一个幸存者入手，找到原索引。

class Solution {
    public int lastRemaining(int n, int m) {
        // 定义最后一个幸存者的位置，为0
        int p = 0;
        // 逆推过程
        for(int i = 1; i < n;i++){
            p = (p + m) % (i + 1);
        }
        return p;
    }
}