二叉树前序-中序-后序遍历（递归、栈结构）

推荐两个up主：

happygirlzt

图灵星球Turing Planet及其个人网站

本博文参考的视频：

二叉树前序中序后序遍历（深度优先搜索）的迭代解法

本博文参考的文章：

数据结构图文解析之：栈的简介及C++模板实现

动画演示+三种实现 94. 二叉树的中序遍历

---

栈的相关概念

栈顶与栈底：允许元素插入与删除的一端称为栈顶，另一端称为栈底。

压栈：栈的插入操作，叫做进栈，也称压栈、入栈。

弹栈：栈的删除操作，也叫做出栈。

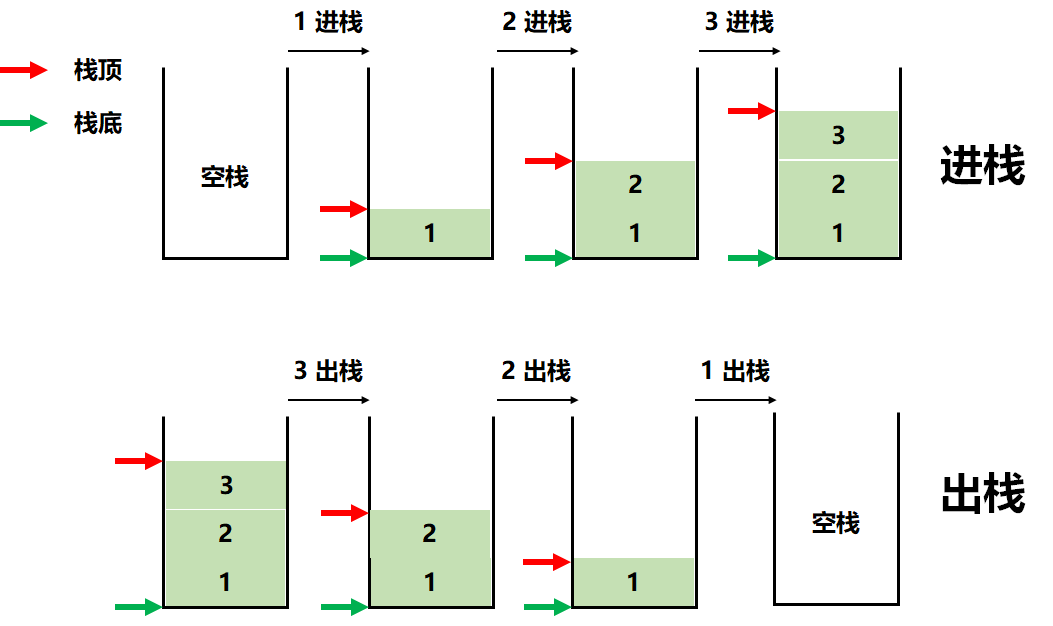
压栈的过程中，栈顶的位置一直在“向上”移动，而栈底是固定不变的。

出栈的过程中，栈顶的位置一直在“向下”移动，而栈底是固定不变的。

先进后出原则

压栈顺序：1—>2—>3

出栈顺序：3—>2—>1

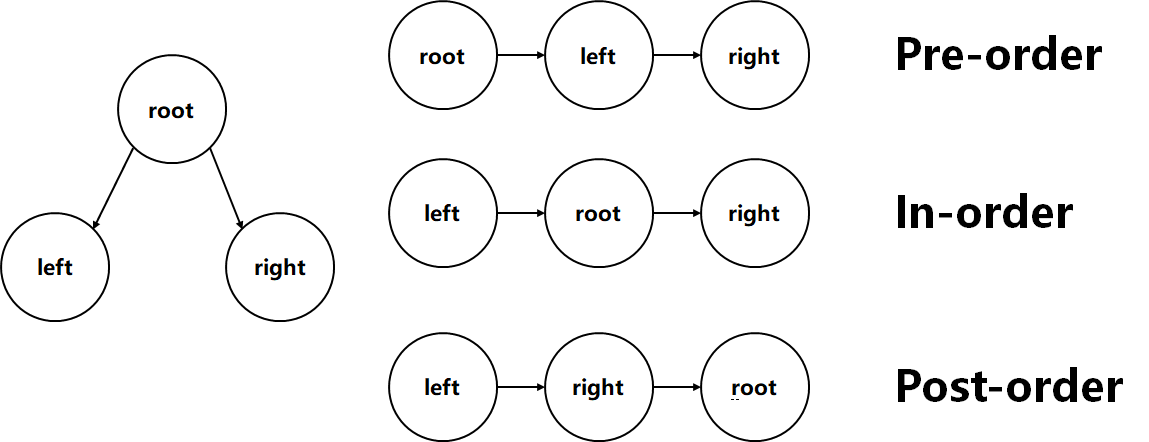
前序遍历（pre-order）

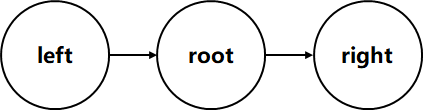
先打印root节点，再打印left节点，最后打印right节点。

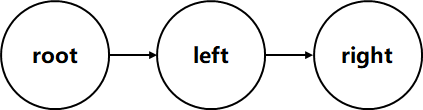
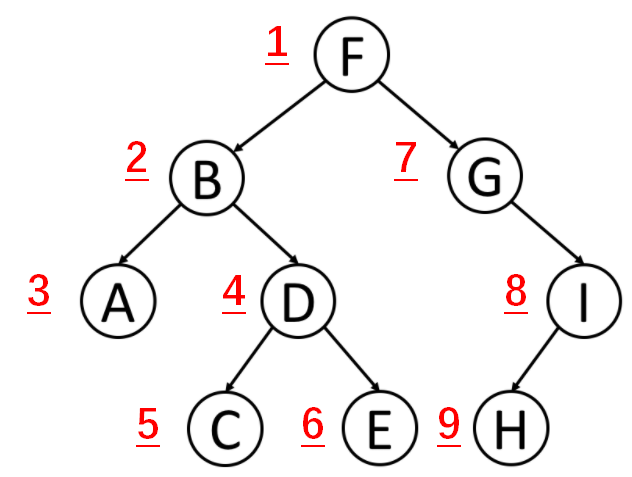
输出为：F B A D C E G I H

递归（recursion）

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if(root == null) return res;
        res.add(root.val); // root
        preorderTraversal(root.left); // left
        preorderTraversal(root.right); // right
        return res;
    }
}

辅助栈

原则：right先入栈，left后入栈（先打印left，后打印right）

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;

        Deque<TreeNode> stack = new ArrayDeque<>();
        stack.push(root);

        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            // 先打印root值
            res.add(node.val);

            if(node.right != null){
                // right先进栈（后打印）
                stack.push(node.right);
            }

            if(node.left != null){
                // left后进栈（先打印）
                stack.push(node.left);
            }
        }
        return res;
        
    }
}

中序遍历（in-order）

先打印left节点，再打印root节点，最后打印right节点。

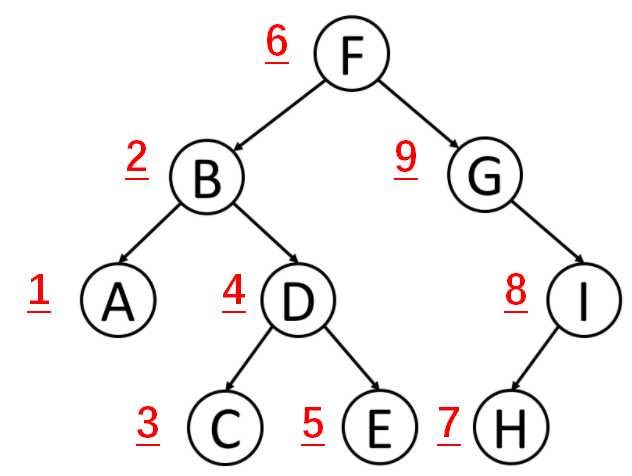
输出为：A B C D E F G H I

递归（recursion）

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if(root == null) return res;
        inorderTraversal(root.left); // left
        res.add(root.val); // root
        inorderTraversal(root.right); // right
        return res;
    }
}

辅助栈

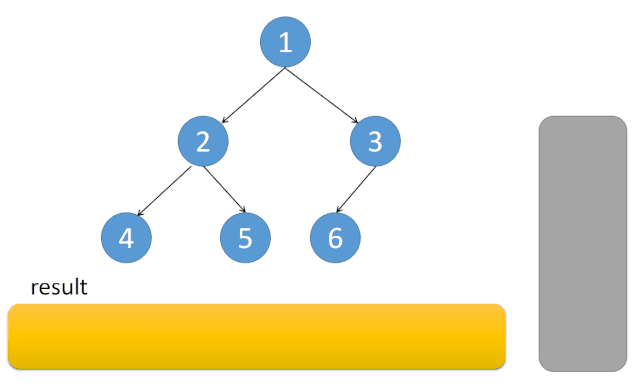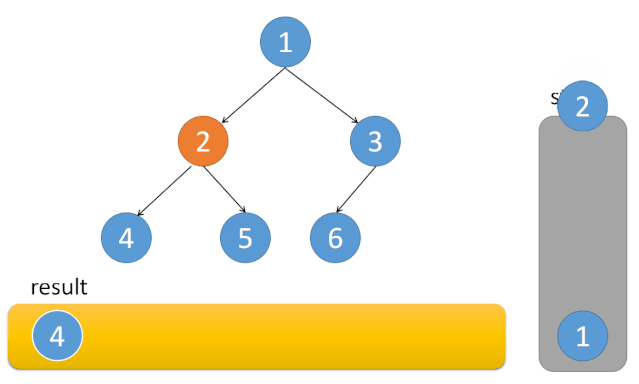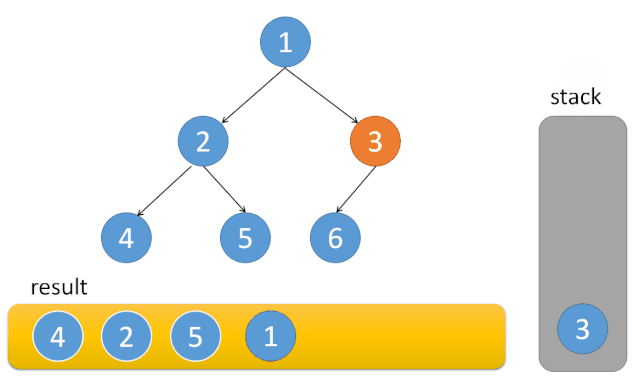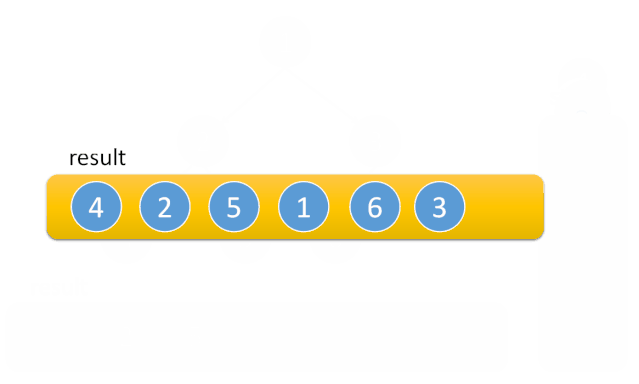
动图来源：动画演示+三种实现 94. 二叉树的中序遍历

class Solution {
    
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;
        Deque<TreeNode> stack = new ArrayDeque<>();
        while(!stack.isEmpty() || root != null){
            // 不断地将左节点压入栈
            // 模拟递归调用
            while(root != null){
                stack.push(root);
                root = root.left;
            }
            //当前节点为空，说明左边走到头了，从栈中弹出节点并保存
			//然后转向右边节点，继续上面整个过程
            // tmp第一次弹出的就是节点4
            TreeNode tmp = stack.pop();
            res.add(tmp.val);
            root = tmp.right;
        }
        return res;
    }
}

后序遍历（post-order）

先打印left节点，再打印right节点，最后打印root节点。

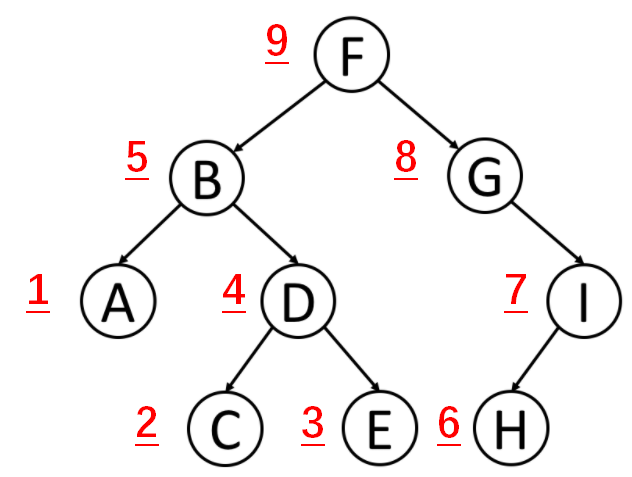
输出为：A C E D B H I G F

递归（recursion）

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if(root == null) return res;
        postorderTraversal(root.left);       
        postorderTraversal(root.right);
        res.add(root.val);
        return res;

    }
}

辅助栈

后序遍历利用辅助栈的方式和前序遍历类似

前序遍历要求：root—>left—>right

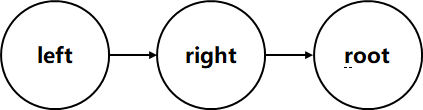
后序遍历要求：left—>right—root

可以理解为先将先序遍历的left和right顺序互换，然后整体反转，得到后序遍历结果。

因此left先进栈，right后进栈。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        LinkedList<Integer> res = new LinkedList<>();
        if(root == null) return res;

        Deque<TreeNode> stack = new ArrayDeque<>();
        stack.push(root);

        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            // 添加顺序与add相反
            res.addFirst(node.val);

            // 以下步骤与前序遍历相反
            if(node.left != null){
                // left先进栈（后打印）
                stack.push(node.left);
            }

            if(node.right != null){
                // right后进栈（先打印）
                stack.push(node.right);
            }
        }
        return res;

    }
}