LeetCode-青蛙跳台阶问题

题目要求

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

示例 2：

输入：n = 7
输出：21

示例 3：

输入：n = 0
输出：1

原题链接：剑指 Offer 10- II. 青蛙跳台阶问题

解题过程

其实这个题和斐波那契数列的思想差不多。

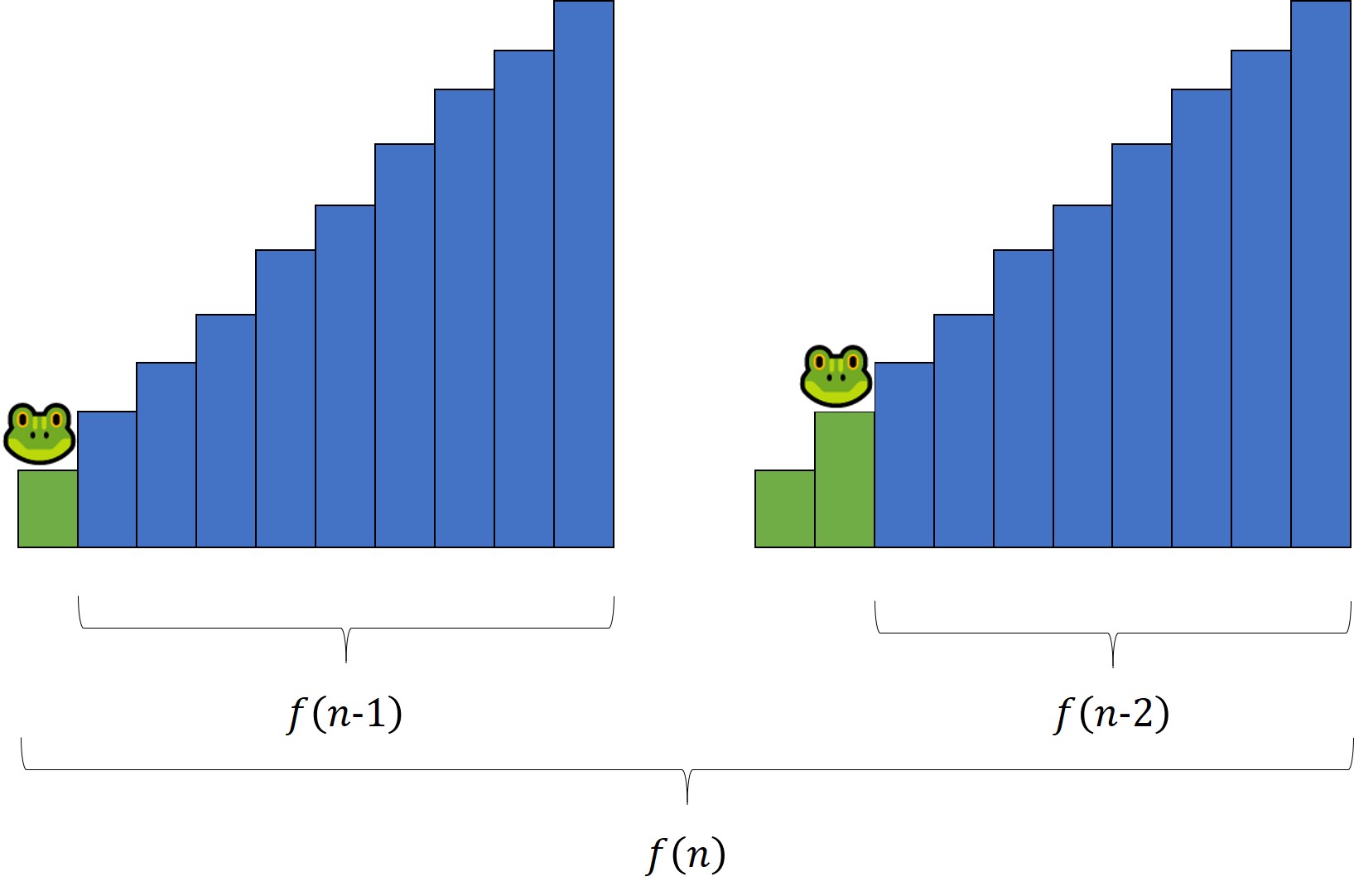
假如青蛙第一次跳了1个台阶，那么剩下来的跳法便是$f(n-1)$次；

假如青蛙第一次跳了2个台阶，那么剩下来的跳法便是$f(n-2)$次；

最终的所有跳法$f(n)=f(n-1)+f(n-2)$。

考虑到时间效率，递归方法会造成大量的重复计算，所以考虑动态规划方法，处理方法和斐波那契数列一样。

class Solution {
    public int numWays(int n) {
        int a = 1;
        int b = 1;
        int sum;
        for(int i = 0; i < n; i++){
            sum = (a + b)%1000000007;
            b = a;
            a = sum;
        }
        return b;
    }
}

类似题型

LeetCode-斐波那契数列