YuanbaoQiang
0%

LeetCode-二维数组中的查找

Posted on In Valine:
Symbols count in article: 923 Reading time ≈ 1 mins.

题目要求

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。 

1
2
3
4
5
6
7
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

原题链接：剑指 Offer 04. 二维数组中的查找

解题过程

暴力解法

遍历数组所有元素，时间复杂度为$O(N*M)$，显然是不可取的。

不回头走法（引入标志数）

面试题04. 二维数组中的查找（左下角标志数法，清晰图解）

给定数组是自左向右递增，自上而下递增。

左下角元素为行最小，列最大单元

右上角元素为行最大，列最小单元

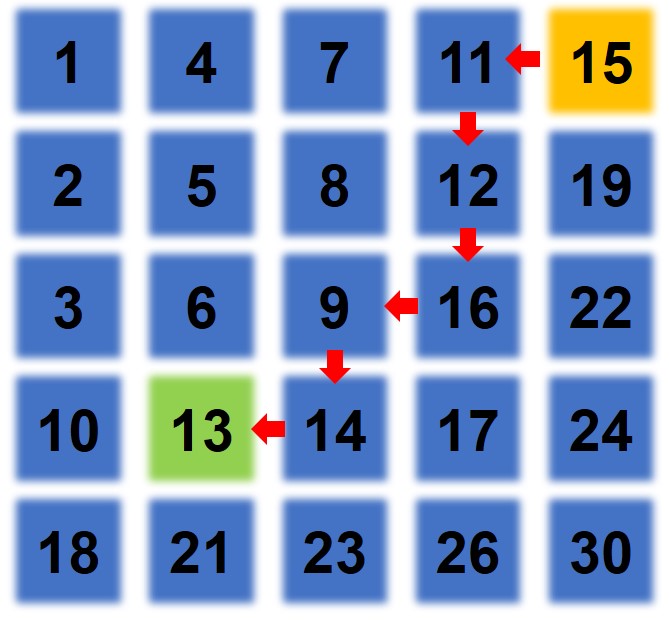
以右上角元素为起始点查询，x为行，y为列。

如果matrix[x][y] > target，则target一定在左侧，y—;

如果matrix[x][y] < target，则target一定在下方，x++；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        // 排除特殊情况
        if (matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int rows = matrix.length;
        int cols = matrix[0].length;
        int x = 0;
        int y = cols - 1; // matrix[x][y] 最一开始为数组右上角元素
        while (x < rows && y >= 0) {
            if (matrix[x][y] > target) {
                y--;
            } else if (matrix[x][y] < target) {
                x++;
            } else {
                return true;
            }
        }
        return false;
    }
}

时间复杂度：$O(M+N)$

空间复杂度：$O(1)$