LeetCode-斐波那契数列（递归、动态规划）

题目要求

写一个函数，输入n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

$ F(0) = 0, \ F(1) = 1 $

$ F(N) = F(N-1) + F(N-2) $, 其中$N>1$

斐波那契数列由0和1开始，之后的斐波那契数就是由之前的两数相加而得出。答案需要取模1e9+7（1000000007），如计算初始结果为1000000008，请返回1。

---

原题链接：剑指 Offer 10- I. 斐波那契数列

相似题目：509. 斐波那契数

解题过程

大数越界： 随着 n 增大, f(n) 会超过 Int32 甚至 Int64 的取值范围，导致最终的返回值错误，所以题目中会有取模操作。

递归

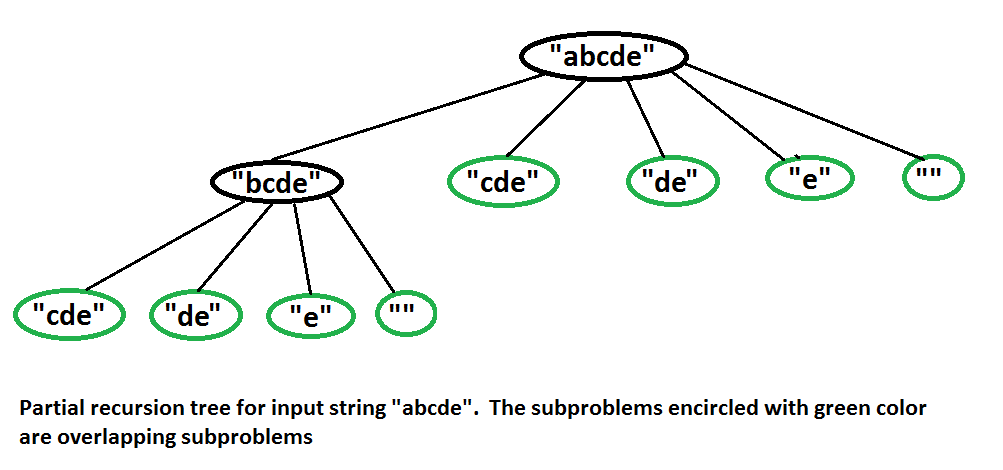
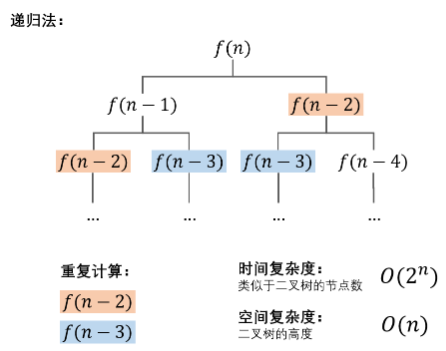
递归方式计算斐波那契数列虽然代码量简单，但是其时间复杂度为$O(2^N)$，影响计算效率，在此不太建议。

非递归

for循环

此方法计算时间还可以，但是很占内存，原因就在于定义了一个动态数组，内存占用随着n的增大而增大。

时间复杂度：$O(n)$

空间复杂度：$O(n)$

class Solution {
    public int fib(int n) {
        int[] arr = new int[n+1];
        if(n==0){
            return 0;
        }else{
            arr[0]=0;
            arr[1]=1;
            for(int i = 2; i <= n; i++){
                arr[i] = (arr[i-1] + arr[i-2]) % 1000000007;
            }
            return arr[n];
        }

    }
}

动态规划

参考：面试题10- I. 斐波那契数列（动态规划，清晰图解）

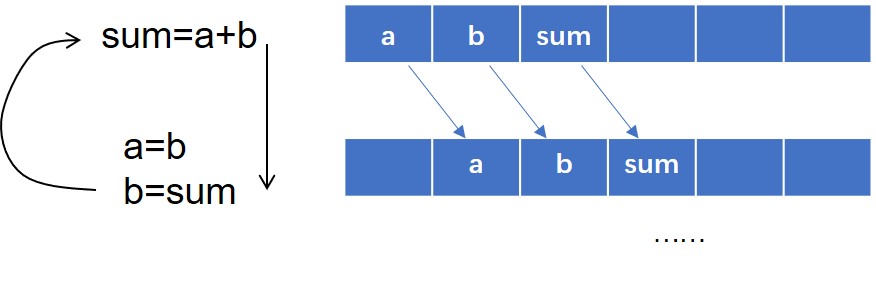
空间复杂度优化，由于在整个计算过程中，第三项只和前两项之和有关，而最终结果只需要最后一个结果，因此对于对数组进行动态定义是会占用多余的空间。只需定义三个局部变量即可：a, b, sum。

此时时间复杂度为$O(n)$，空间复杂度为$O(1)$。

class Solution {
    public int fib(int n) {
        int a = 0;
        int b = 1;
        int sum;
        
        for(int i = 0; i < n; i++){
            sum = (a+b) % 1000000007;
            a = b;
            b = sum;
        } 
        return a; 
            
    }
}