递归——迭代是人,递归是神🙆♂️
To Iterate is Human, to Recurse, Divine. ——— L. Peter Deutsch
递归是指在函数的定义中使用函数自身的方法,递归一定要向已知方向递归,否则这种递归就变成了无穷递归,类似于死循环。
目前刚接触递归,但是已经感觉它的难度了…后续持续补充相关算法,加深理解😜。
1-n之和
1 | /** |
n!
1 | public int getProduct(int n){ |
斐波那契数列(Fibonacci sequence)
表达式:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
0、1、1、2、3、5、8、13、21、34、……
1 | /** |
汉诺塔问题
有三根杆子A,B,C。A杆上有 N 个 (N>1) 穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆:
- 每次只能移动一个圆盘;
- 大盘不能叠在小盘上面。
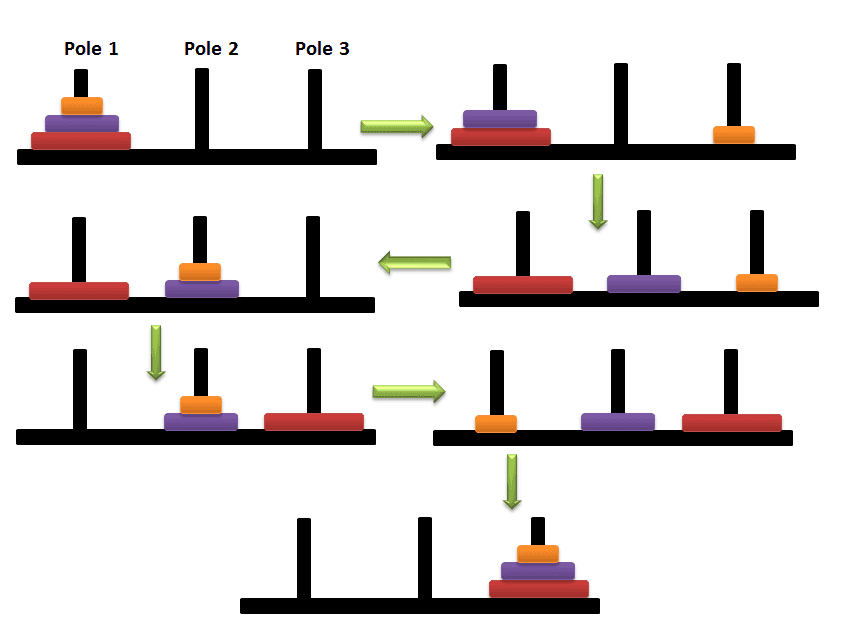
三层
四层
十层

……
个人理解
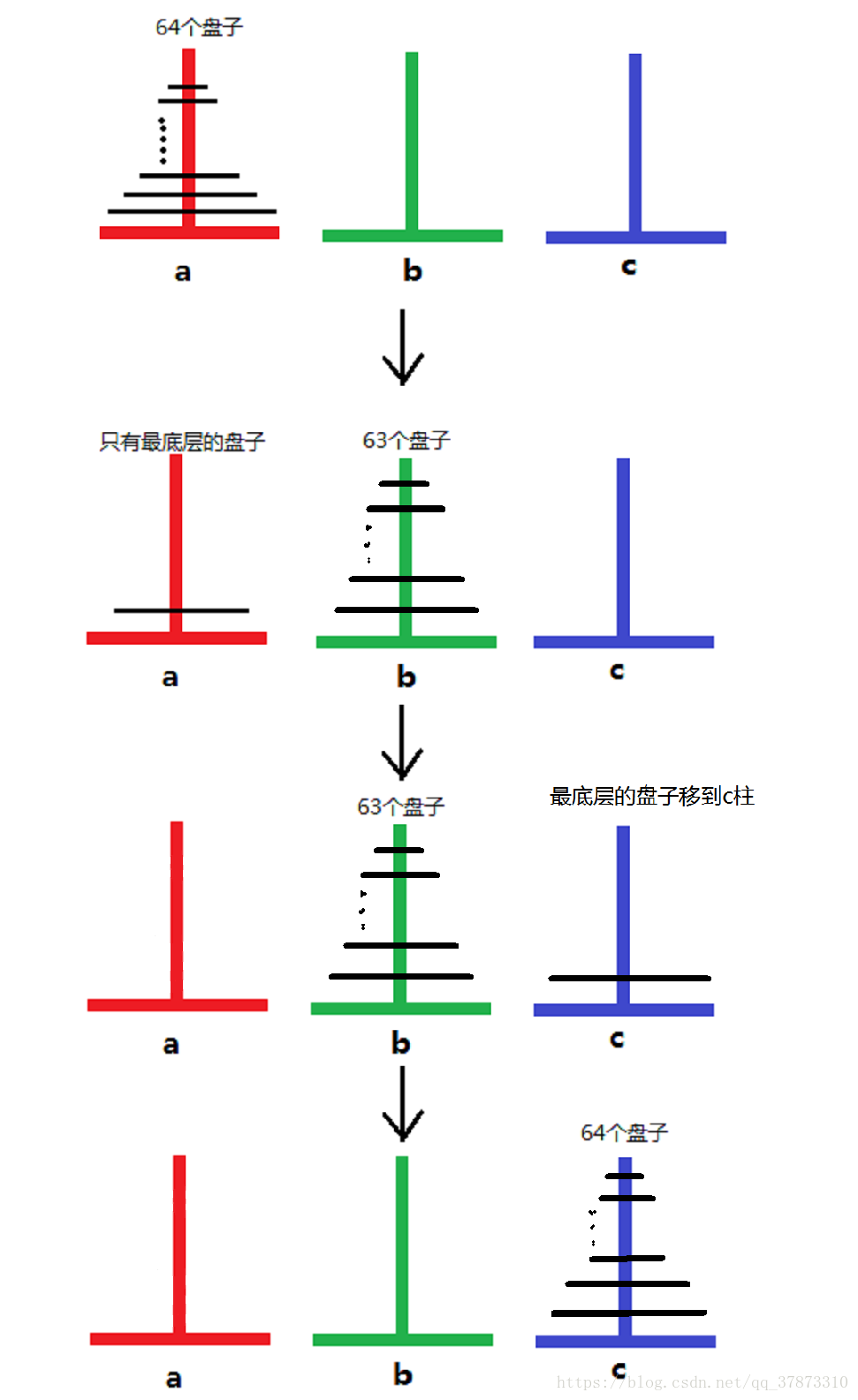
其实整个过程主要是三个主要流程:
- 将n-1个圆盘从A转移到B;(A—>B)
- 将最大的圆盘从A转移到C;(A—>C)
- 此时的B上的n-1个圆盘和初始状态的A是一样的,再次进行1-2步骤。(B—>C)
例如以下的例子,可以将63个圆盘堪称一个整体,依次类推。
代码如下:
1 | /** |